X by the substitution of du, d u, and be left with an even number of cosine powers Use cos2x = 1−sin2x (= 1−u2) cos 2 x = 1 − sin 2 x ( = 1 − u 2) to replace the leftover cosines Both m m and n n are odd Use either 1 1 or 2 2 (both will work) Both m m and n n are even Use cos2x = 1 2(1cos(2x)) cos 2 Sec(x) tan(x) dx = Z 1 sec(x) tan(x) sec2(x) sec(x)tan(x) dx = Z 1 u du for ˆ u= sec( x) tan( ) du= (sec2( x) sec( )tan( ))dx = lnjuj C = lnjsec(x)tan(x)j C Another trick for this is to write R sec(x)dx= R 1 cos2(x) cos(x)dx, and substitute u= sin(x) to get R 1 1 u2 du We will see how to integrate such rational functions in x74 $\begingroup$ I actually prefer Using $\tan$ and $\sec$ because they seem much simpler to me than converting to rational functions $(\tan x)' = \sec^2 x$ and $(\sec x)' = \sec x \tan x$ go handinhand $\endgroup$ – Dylan Sep 16 '15 at 21
Q Tbn And9gcr1hzoptmtla Kxxcxtkksx7s8mu4uts6 74qmdsrnv4xuqmwwt Usqp Cau
Integrate tan^2x sec^2x/1-tan^6x
Integrate tan^2x sec^2x/1-tan^6x-0 votes 1 answer Evaluate the following integrals ∫cos 2x/(cos x sin x)^2dx sec^2xdx=dt I=integral(t2/(1t^3)dt let t^3=z 3t^2dt=dz I=1/3int(dz/(1z)) as int(1/1z)= log(1z) I= log(1z) c= log(1t^3)c I= log(1tan^6x)c



bestpictjcry Tan 2x Tan 2x
How do I evaluate the indefinite integral #int(tan^2(x)tan^4(x))^2dx# ? In this section we are going to look at quite a few integrals involving trig functions and some of the techniques we can use to help us evaluate them Let's start off with an integral that we should already be able to do ∫cosxsin5xdx = ∫u5du using the substitution u = sinx = 1Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!
Sin^2 x = 1cos(2x)/2;Tan^2xsec^2x/1tan^6x Ask questions, doubts, problems and we will help youIntegrate 1/(cos(x)2) from 0 to 2pi;
If you let u=tanx in integral (tan^2)x you get integral u^2 dx which is not (u^3)/3 c since du= sec^2x dx1 tan^2 x = sec^2;Math Cheat Sheet for Integrals This website uses cookies to ensure you get the best experience By using this website, you agree to our Cookie Policy Learn more Accept Solutions Graphing \int \sec^2(x) dx=\tan(x) \int \csc^2(x) dx =\cot(x) \int \frac{1}{\sin^2(x)}dx=\cot(x) \int \frac{1}{\cos^2(x)}dx=\tan(x)
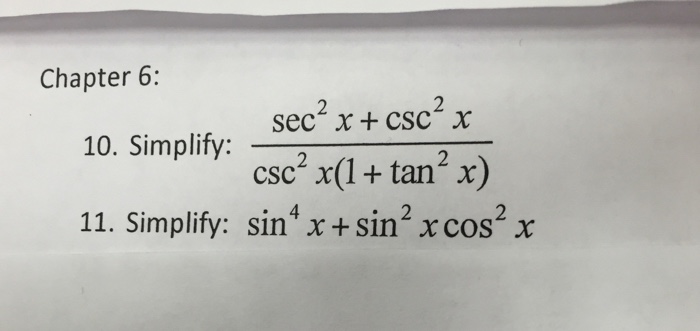



Tan2x Sec2x ただの悪魔の画像




How To Integrate 2x Sec 3 X 2 3 Tan X 2 3 Quora
\∫\sec^n x\,dx=\frac{1}{n−1}\sec^{n−2}x\tan x\frac{n−2}{n−1}∫\sec^{n−2}x\,dx\ \∫\tan^n x\,dx=\frac{1}{n−1}\tan^{n−1}x−∫\tan^{n−2}x\,dx\ The first power reduction rule may be verified by applying integration by parts The second may be verified by following the strategy outlined for integrating odd powers of \(\tan2 If n is odd, then using substitutions similar to that outlined above we have ∫sinmxcosnx dx = ∫um(1 u2)k 𝑑u, where u = sinx and du = cosx dx 3 If both m and n are even, use the halfangle identities cos2x = 1 cos(2x) 2 and sin2x = 1 cos(2x) 2 to reduce the degree of the integrandLearn vocabulary, terms, and more with flashcards, games, and other study tools




Evaluate Int Sec 2x 1 Tan 2x Dx




Int Sec 2x Tan 2x 4 Dx Maths Questions
The correct option (c) tan –1 (tan 2 x) Explanation ∫(sin2x dx)/(sin 4 x cos 4 x) = ∫(2sinx cosx dx)/(sin 4 x cos 4 x) = ∫(2 tanx ∙ sec 2 x)/(1 tan 4 x) dx Let tan 2 x = t ∴ 2tanx ∙ sec 2 x ∙ dx = dt ∴ I = ∫dt /(1 t 2) = tan –1 (t) c ∴ I = tan –1 (tan 2 x) cSin^2x = 1 cos(2x)/2; The integral ∫(sec^2x/(secx tanx)^9/2)dx equals (for some arbitrary constant K) asked in Integrals calculus by Rozy ( 418k points) indefinite integration
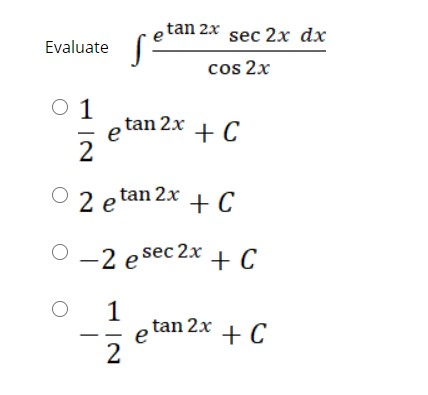



Answered Tan 2x Sec 2x Dx Evaluate Cos 2x O 1 Bartleby




Integration Trig Identities Ppt Download
Let's look at the relationship between tangent and secant We have the following Pythagorean identity tan2x1 = sec2x tan 2 x 1 = sec 2 x Likewise they are related by theirFree integral calculator solve indefinite, definite and multiple integrals with all the steps Type in any integral to get the solution, steps and graph This website uses cookies to ensure you get the best experienceIntegration of tan^2x sec^2x/ 1tan^6x dx Ask questions, doubts, problems and we will help you



What Is Math Int Tan 2 2x Dx Math Quora




Find The Integrals Of The Functions Tan3 2x Sec 2x Mathematics Shaalaa Com
The formula sin 2(x) cos2(x) = 1 and divide entirely by cos (x) one gets tan 2 (x) 1 = sec 2 (x) One case see that in the case where you have an even (nonzero) power of sec(x) the rst is possible1 tan^2x = sec^2x;Cos^2x = 1 cos(2x)/2 integral sec^6(x) dx integral cos^5(x) dx integral sec^3(2x) sin(2x)dx




Calculus Integration Strategy Trig Tan 6x Sec 4x Even Power Products Youtube




Midterm 17 18 Questions And Answers Studocu
Integral of tan^4(x)*sec^6(x), calculus 2 trig integral, blackpenredpen integralwwwblackpenredpencom/calc2 Integrate $$\int \tan^6x\sec^3x \ \mathrm{d}x$$ I tried to split integral to $$\tan^6x\sec^2x\sec x$$ but no luck for me Help thanks int(1tan^2(x))sec^2(x)dx We know 1tan^2(x) = 1/cos^2(x) sec^2(x) = 1/cos^2(x) So we have int1/cos^4(x)dx Let's t = tan(x) and dt = 1/cos^2(x)dx We have int1/cos^2(x)dt int1tan^2dt int1t^2dt t1/3t^3 tan(x)1/3tan^3(x)C




Ex 9 4 4 Find General Solution Sec2 X Tan Y Dx Sec2y




Qprove That Tan X 2 Tan 2x 4 Tan 4x 8 Cot 8x Cot X Mathematics Topperlearning Com Blpusg55
The cos2(2x) term is another trigonometric integral with an even power, requiring the powerreducing formula again The cos3(2x) term is a cosine function with an odd power, requiring a substitution as done before We integrate each in turn below ∫cos2(2x) dx = ∫ 1 cos(4x) 2 dx = 1 2 (x 1 4sin(4x)) CIntegral of Tangent to the Sixth Power (tan^6 (x)) by Mark (US) Here's another example submited and solved by Mark Here we just use the technique described when we have tangent and secant We just do the basic substitutions Return to Trigonometric IntegralsIntegral of sec^6 x/tan^2 x dx trigonometry formulae integration formulae Articles




Ex 7 3 16 Integrate Tan 4 X Teachoo Maths Ex 7 3



bestpictjcry Tan 2x Tan 2x
Integrate x^2 sin y dx dy, x=0 to 1, y=0 to pi;See all questions in Integrals of Trigonometric Functions Integrals Class 12 Important Extra Questions Maths Chapter 7 by Prasanna Here we are providing Class 12 Maths Important Extra Questions and Answers Chapter 7 Integrals Class 12 Maths Important Questions are the best resource for students which helps in Class 12 board exams



Evaluate Sec 2 X 16 Tan 2 X Dx Sarthaks Econnect Largest Online Education Community




Answered Evaluate The Following Integral Tan X Bartleby
Answer to Integrate the following 1 csc^3(x)dx 2 tan^3(2x)sec^3(2x)dx 3 sin(6x)cos(2x)dx 4sin(6x)cos(2x)dx 5 sin^4(3x)cos^3(3Cos^2 x = 1cos (2x)/2 integral sec^6 (x)dx integral cos^5(x) dxAnswer to Integrate the trigonometric integral integral of sec^2(x)/(1tan(x)) dx evaluated from 0 to pi/4 By signing up, you'll get thousands of




Evaluate Int Sec 2x 1 Tan 2x Dx




Integral Of Sec 2 X Sqrt 1 Tan 2 X Using The Arcsine Function Math Videos Maths Exam Calculus
Dx$$ to get the solution in the form of $$\large\frac{2}{7}\sec^{7/2}x \frac{2}{3}\sec^{3/2}x c$$ I tried takingEvaluate the integral ∫sec^6x tan x dx 1 answer Evaluate ∫cos^1(1 tan^2x/1 tan^2x) asked Aug 2 in Indefinite Integral by Dheeya (304k points) indefinite integral;Useful Trigonometric Identities sin^2 x cos^2 x = 1;



Http Www Math Ncku Edu Tw Rchen 18 19 teaching Chapter 7 Stewartcalc8 07 02 Pdf




The Value Of Int Tan 3 2x Sec 2x Dx Is Equal To Youtube
∫tan3 xsin2 3x(2 sec2 xsin2 3x 3 tan x sin 6x) dx for x ∈ π/6,π/3 is equal to (1) 9/2 (2) 1/9 (3) 1/18 (4) 7/184 Chapter 10 Techniques of Integration EXAMPLE 1012 Evaluate Z sin6 xdx Use sin2 x = (1 − cos(2x))/2 to rewrite the function Z sin6 xdx = Z (sin2 x)3 dx = Z (1− cos2x)3 8 dx = 1 8 Z 1−3cos2x3cos2 2x− cos3 2xdx Now we have four integrals to evaluate Z 1dx = x and Z Calculus 2, integral of (1tan^2x)/sec^2x, integral of cos(2x)




Differentiate The Following W R T X Tan 1 X 1 6x 2 Cot 1 1 10x 2 7x



Integral Of Tan 2x Secx
Trigonometric Simplification Calculator \square!To avoid ambiguous queries, make sure to use parentheses where necessary Here are some examples illustrating how to ask for an integral integrate x/(x1) integrate x sin(x^2) integrate x sqrt(1sqrt(x)) integrate x/(x1)^3 from 0 to infinity;\\int \tan^{2}x\sec{x} \, dx\ > <




Tan2x ただの悪魔の画像




Prove Tan X Sec X 1 Tan X Sec X 1 1 Sin X Cos X Brainly In
Let mathT = \displaystyle \int \frac{\tan{\left(\frac{1}{x}\right)}}{x^2} \,\mathrm dx/math Let mathu = \frac{1}{x}\ \therefore \mathrm du = \frac{1}{x^2How do I evaluate the indefinite integral #intx*sin(x)*tan(x)dx# ? Get an answer for 'Evaluate the indefinite integral integrate of (tan(6x))^3(sec(6x))dx' and find homework help for other Math questions at eNotes `int (sec(2x) tan(2x)) dx` Find the




Powers Of Trigonometric Functions




Integral 1 Tan 2 X Sec 2 X Youtube
Trigonometric Identities sin^2x cos^2x = 1;Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and moreYour substitution is not correct You should still still have a $\sin^3 x$ upstairs However when integrating a product of an even power of $\tan$ with an even power of $\sec$, you can do the following, which takes advantage of the facts that $\tan^2x1=\sec^2 x$ and that the derivative of $\tan x$ is $\sec^2 x$



bestpictjcry Tan 2x Tan 2x
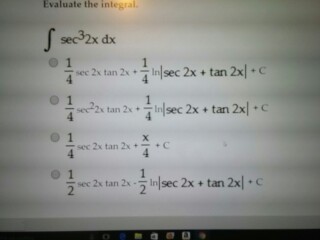



Integral Sec 32x Dx 1 4 Sec 2x Tan 2x 1 4 In Sec Chegg Com
You have already been told about the useful identity $$1\tan^2 x=\frac{1}{\cos^2 x}$$ You may have seen this identity as $$1\tan^2x =\sec^2 x$$ There are slightly tricky things about taking square roots, but they are not a problem in the interval where you are working We end up wanting to find $\int \sec x dx$, or equivalently $\int dx Integral of u^2 is NOT (u^3)/3 c Rather, integral of (u^2)du = (u^3)/3 c In (tan^2)x your 1st mistake is not writing dx Note that dx is NOT always du!!!!!How to solve the following indefinite integral $$\int \tan^{3}x \sec^{3/2}x \;




How Do You Integrate Csc2x Cot2x 2 Dx Socratic




Integration Calculus Notes
The following is a list of integrals (antiderivative functions) of trigonometric functionsFor antiderivatives involving both exponential and trigonometric functions, see List of integrals of exponential functionsFor a complete list of antiderivative functions, see Lists of integralsFor the special antiderivatives involving trigonometric functions, see Trigonometric integralLet u = tan x, du = (sec x)^2 dx, while (sec x)^4 = 1 (tan x)^2^2 = (1u^2)^2 Thus, by substitution, we can simply the integral as = Int u^2 (1 u^2)^2 du = Int (u^6 2u^4 u^2) du = (1/7) u^7 (2/5) u^5 (1/3) u^3 C =




Integration Calculus Notes
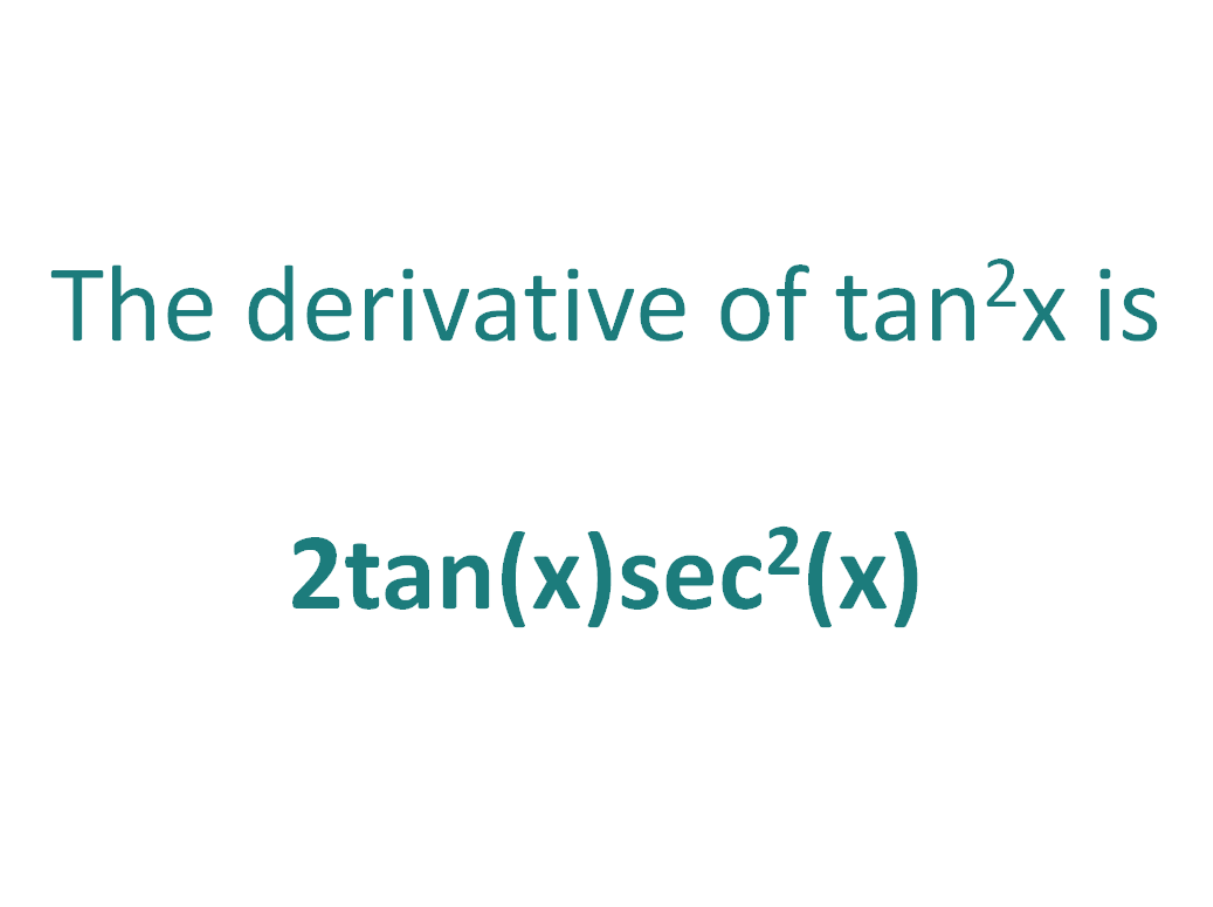



The Derivative Of Tan 2x Derivativeit
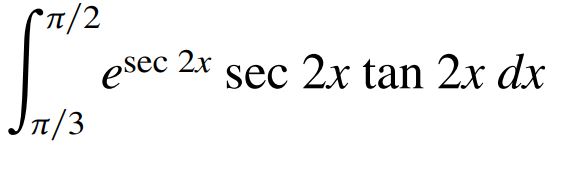



Integral Of Tan 2x Secx



Tan2x Sec2x ただの悪魔の画像
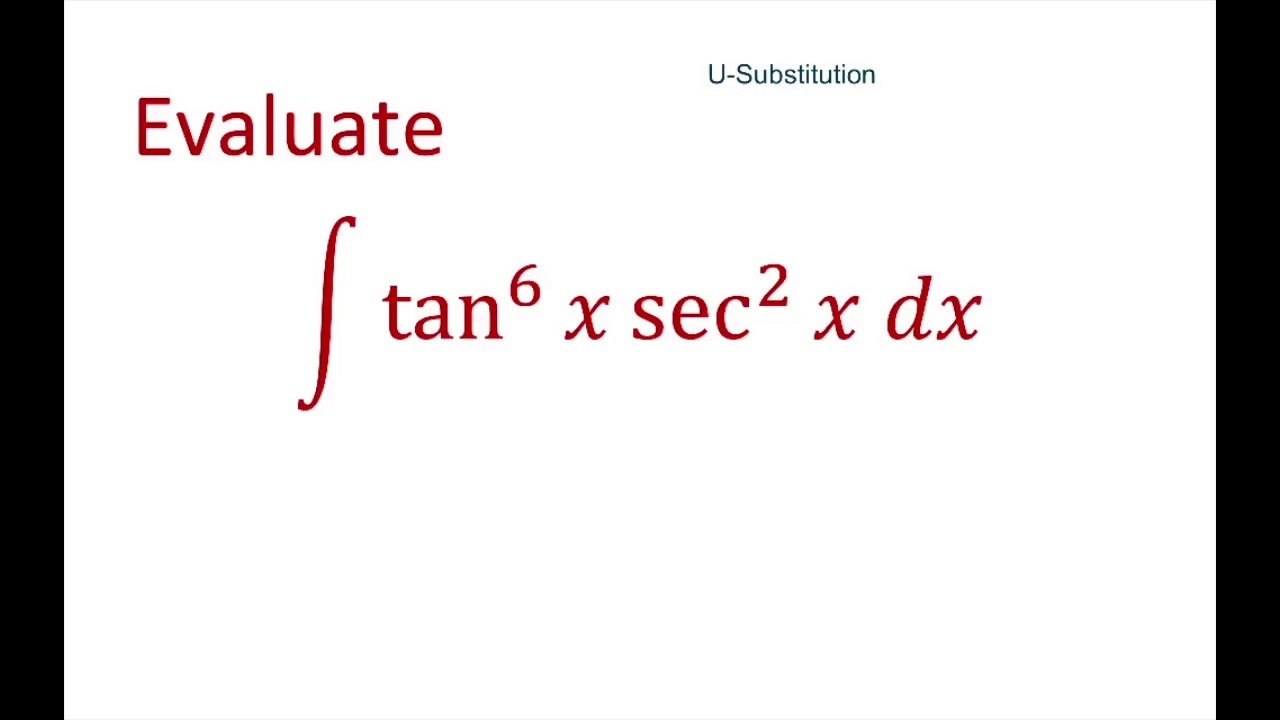



Integrate Tan 6 X Sec 2 X Dx With U Substitution Youtube




Integration Of Tan 2 X Sec 2 X Youtube




Tan2x Sec2x ただの悪魔の画像




What Is The Integration Of Tan 2x Solution Quora




Integral Of E Tan X Sec 2 X Youtube




Intsec 2xlog 1 Sin 2x Dx Tan Xlog 1 Sin 2x 2x K Tan 1 K Tan X Find The Value Of K




Integration Calculus Notes




Integral Sec 2 2x 2 Dx A Tan 2x 2 2 C Chegg Com




Integral Of Tan 2x Secx




Integral 2x Sec X 2 Tan X 2 Dx Integral Cot Theta D Chegg Com



1



How Do You Find The Integral Of 1 Tan 2x Sec 2xdx Socratic




Q28 Tan 2 X Sec 2 X 1 Tan 6 X Dx Integral Of Tan 2 X Sec 2 X 1 Tan 6 X Indefinite Youtube




Integration Calculus Notes




Integration Trig Identities Ppt Download
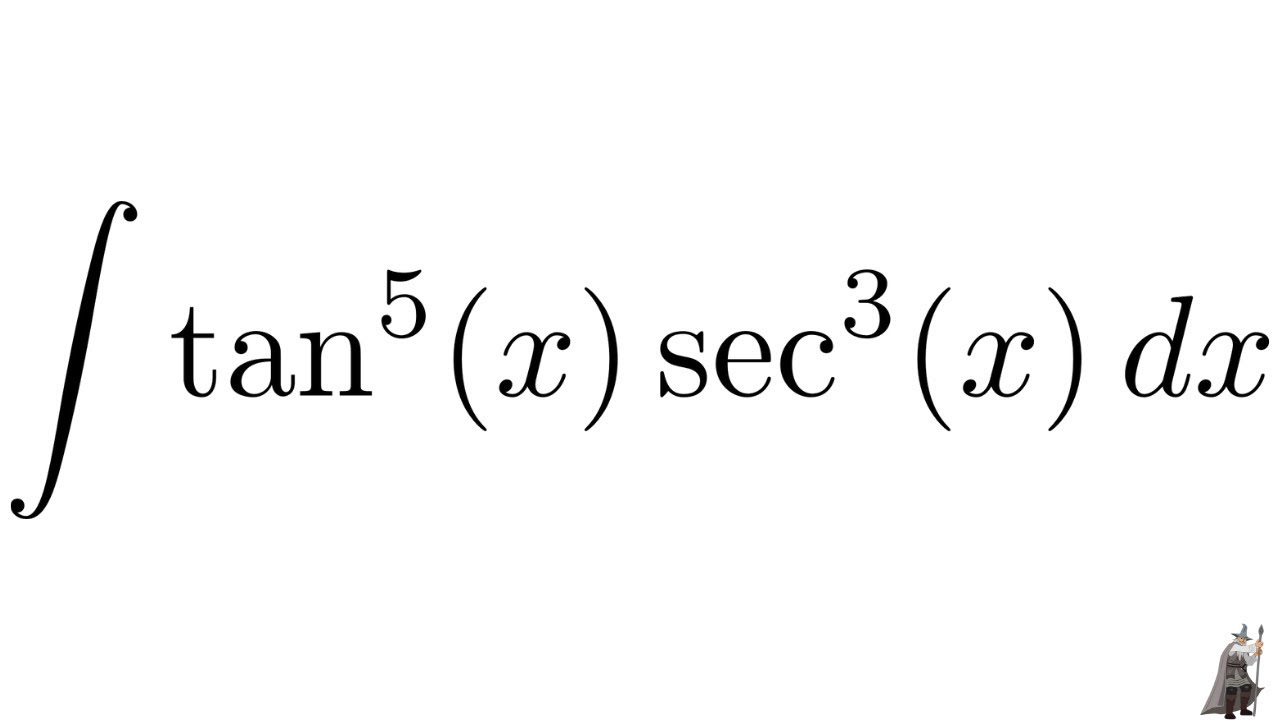



Integral Tan 5 X Sec 3 X Youtube




How Do You Integrate 1 Tan2x Sec2x Dx Socratic



最も欲しかった Tan 2x 1616 Tan 2x 2tanx 1 Tan 2x Jpblopixttnc7



Q Tbn And9gcr1hzoptmtla Kxxcxtkksx7s8mu4uts6 74qmdsrnv4xuqmwwt Usqp Cau




Integration Calculus Notes



1



Evaluate The Following Integrals Tanx Sec 2x 1 Tan 2x Dx Sarthaks Econnect Largest Online Education Community




1 Differentiate The Following With Respect To X Y Chegg Com



Www Math Uh Edu Bekki 1432 Notes 1432 Ps21 Pdf




Integrate Tan 3 2x Sec2x Brainly In



Baixardoc Com Preview Modul Integral Trigonometri 5dbc95df711eb




Trigonometric Integrals




Sec 2 2x 1 Tan2x Youtube
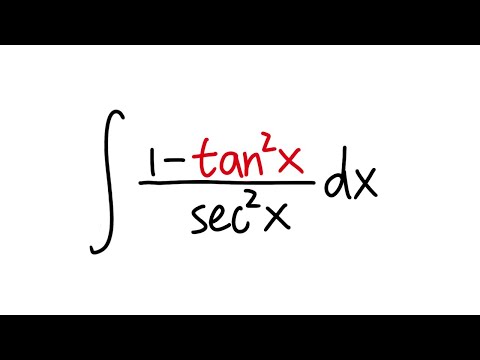



Q45 Integral Of 1 Tan 2x Sec 2x Youtube




Ex 9 4 4 Find General Solution Sec2 X Tan Y Dx Sec2y



Http Www Math Ncku Edu Tw Rchen 18 19 teaching Chapter 7 Stewartcalc8 07 02 Pdf




Oxford Textbook Chapter 6 Full Sol 284 Chapter 6 Indefinite Integration Instant Drill 1 P 6 4 D 4 D 4 D A X 3x X 3 X Dx Dx Dx 4x3 3 D 4 B Course Hero




Tan2x Sec2x ただの悪魔の画像




How To Integrate 2x Sec 3 X 2 3 Tan X 2 3 Quora




Integration Calculus Notes
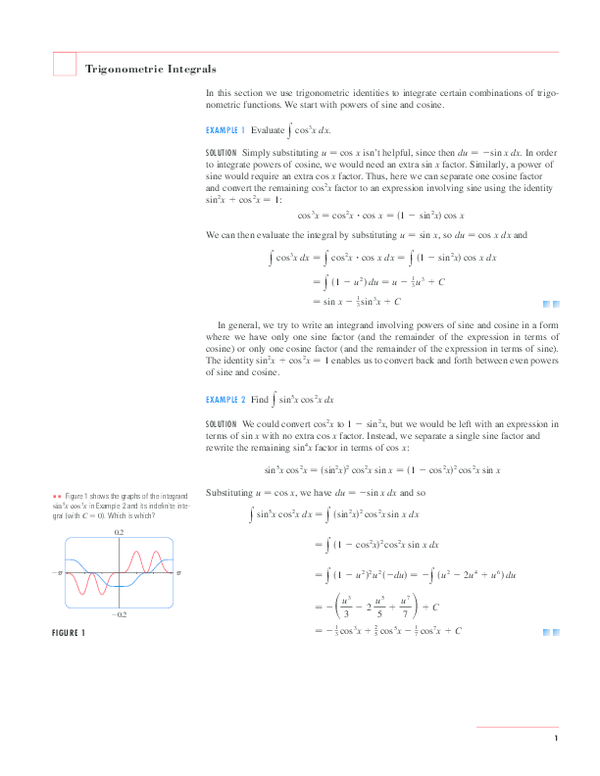



Pdf Trigonometric Integrals Jerome Delen Academia Edu




Powers Of Trigonometric Functions




9 Integral Tan 3xsec 4xdx Integral Chegg Com




Integral Tan 2x Sec 2x 1 Tan 6x Dx Brainly In



If In Tan N X Dx For X 0 P 4 Prove That 1 I2 I4 1 I3 I5 1 I4 I6 1 I5 I7 A P Sarthaks Econnect Largest Online Education Community




Integral Of Cos 2x Tan 3x




Pstrigonometric Equations Trigonometric Functions Equations



1



bestpictjcry Tan 2x Tan 2x




Find The Indefinite Integral Use C For The Constant Chegg Com




Evaluate Int Sec 2x 1 Tan 2x Dx




Cos 2x




14 Lim X Mendekati 0 Dari X Tan 2x 1 Cos 2x Adalah 15 Lim X Mendekati 0 Dari 4x Cos6x 4x Brainly Co Id




Integration Of Tan 1 5x 1 6x 2 Dx Mathematics Topperlearning Com Zb45f7yy



Http Www Unife It Scienze Informatica Insegnamenti Istituzioni Di Matematica Materiale Didattico Esercizi Integrali Prof Ascenzi Del 18 04 18 At Download File




Exercise 7 3 Integrals Of The Functions In Exercises 1 To 22 2 Sin 3x Cos 4x 3 Cos 2x Cos 4x Cos 6x 5 Sin X Cos 6 Sin X Sin 2x




Int Tan 2xsec 2x 1 Tan 6x Dx Youtube
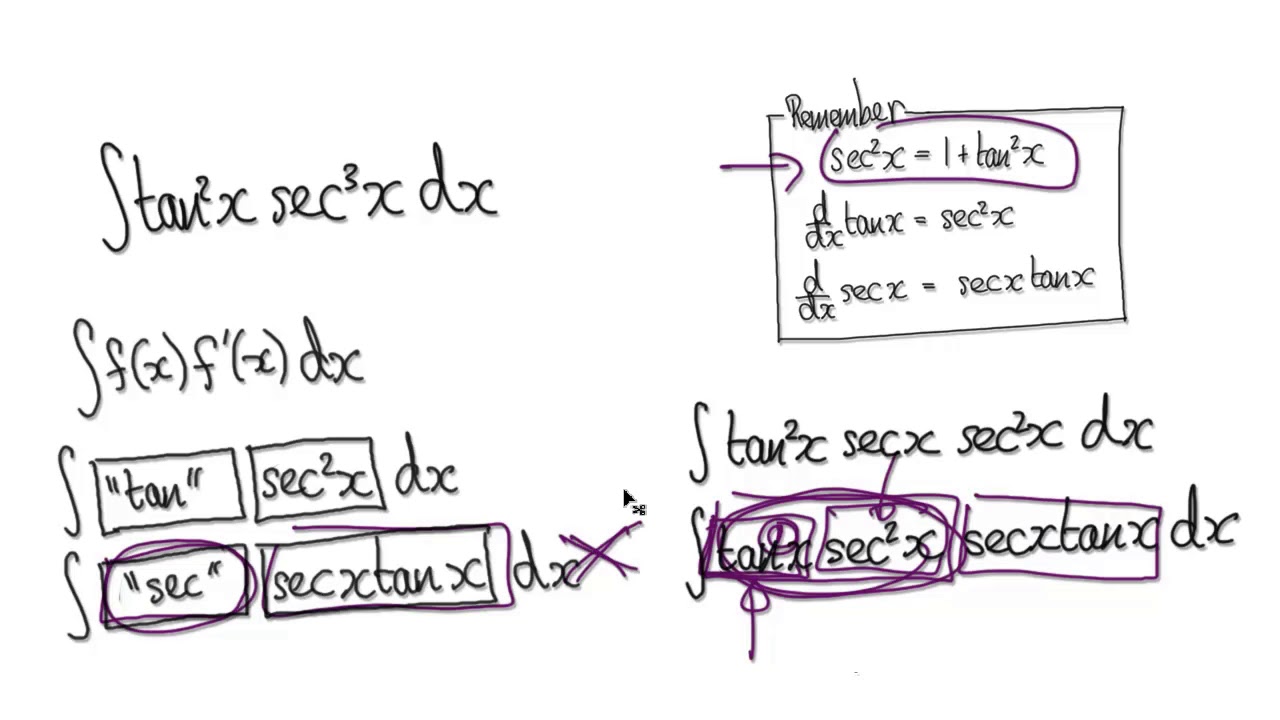



Video 34 6 Integrate Tan 2x Sec 3x Reduction Formula Practice Youtube




Sec 6x Tan 6x 1 2 Tan 2x Sec 2x Important Difficult Trigonometric Identity Youtube



Integral Of Sec 6 X Tan 2 X Dx



How To Integrate X Tan 2 X Dx Quora
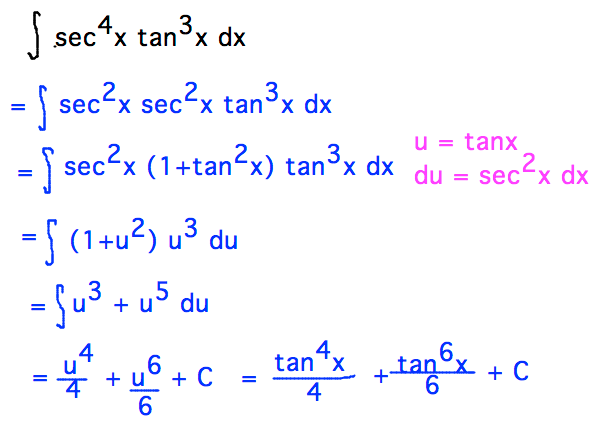



Geneseo Math 222 01 Trigonometric Integration




Tan2x Sec2x ただの悪魔の画像



Http Www Unife It Scienze Informatica Insegnamenti Istituzioni Di Matematica Materiale Didattico Esercizi Integrali Prof Ascenzi Del 18 04 18 At Download File




Ex 9 4 4 Find General Solution Sec2 X Tan Y Dx Sec2y




Evaluate Int Sec 2x 1 Tan 2x Dx




Misc 32 Definite Integral X Tan X Sec X Tanx Miscellaneous



Integral Of Sec 6 X Tan 2 X Dx



Evaluate Sec 2 X Tan 3 X 4 Tan X Dx Sarthaks Econnect Largest Online Education Community




Integral Of Tan 2 X Sec X Youtube




Tan2x Sec2x ただの悪魔の画像



What Is Math Int Tan 2 2x Dx Math Quora



Http 1 160 97 198 8080 Xmlui Bitstream Handle 8 2 chapter i V Pdf Sequence 2
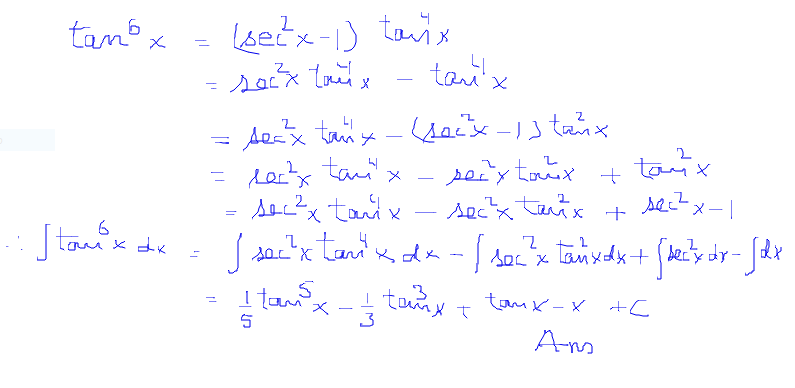



What Is The Integral Of Tan X 6 Socratic




12 Evaluate The Integral Tan 2x 1 Sec 2x 1 Dx Chegg Com



0 件のコメント:
コメントを投稿